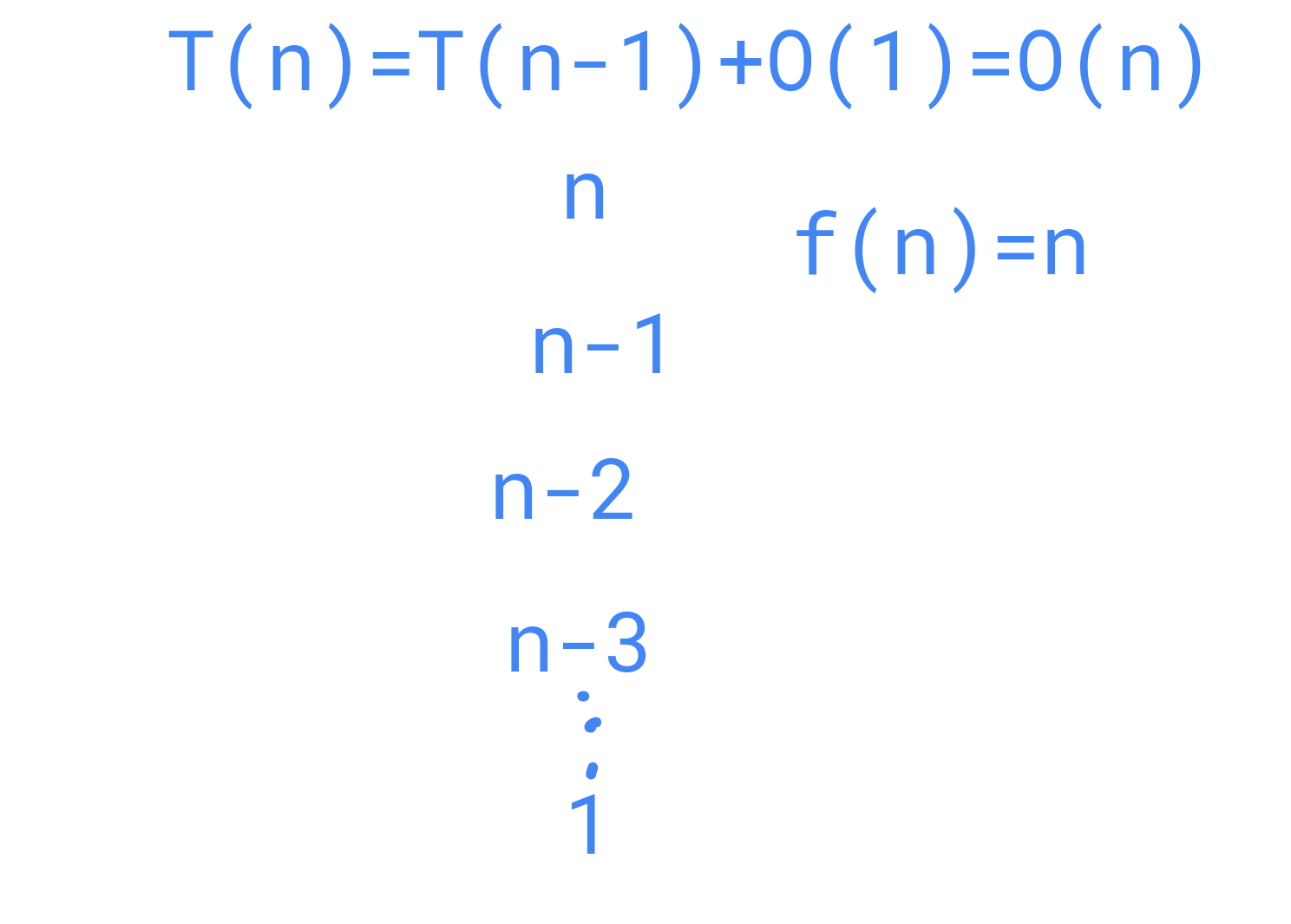Introducción

Sílabo

Se provee una primera etapa de abstracción y razonamiento lógico matemático para identificar las limitaciones de los modelos actuales de computación. Esto se enmarca en el área de la teoría de la computación, la cual se encarga de establecer los fundamentos de las ciencias computacionales de manera formal y realizar un análisis lógico-matemático de las soluciones algorítmicas propuestas para diferentes problemáticas, así como de proponer soluciones alternativas utilizando técnicas avanzadas de diseño de algoritmos.

Programa de unidad de aprendizaje.

Prefacio

Curso impartido en la UABC. Revisado por el Dr. Everardo Gutiérrez López y escrito por su alumno Carlos Eduardo Sánchez Torres.

Este texto y sus recursos se rigen bajo la licencia CC BY-NC-SA 4.0.

Si estas viendo estas notas como PDF u otros formatos, puedes encontrar una versión web en:

https://sanchezcarlosjr.com/UABC Algoritmos 38fac5ca34e740719b43673db9f8b918

Una versión en inglés y más actualizada:

https://carlos-eduardo-sanchez-torres.sanchezcarlosjr.com/Algorithms-937311965b00408c9a849de21750b50a

Recursos

Ecosistema

Esta curso se contexualiza en Ciencias Computacionales:

• Computación
  • Teoria de la computación
    • Análisis y diseño de Algoritmos

ACM Computing Classification System

Curso fundamental para ¿Qué es lo que sigue? ¿Cuál es el estado del arte?

Si te interesan los retos y las matemáticas:

• https://projecteuler.net/. Algunas soluciones explicadas

Si te interesa el open source:

Ambos eventos abren convocatoria a inicio de año y debes pasar por una serie de filtros.

• Google Summer of Code. -te pagan por contribuir y ganas experiencia-.

• Google Season of docs.

Si te interesa participar en programación competitiva -nivel universitario-:

• ICPC

• ICPC México: https://blogs.iteso.mx/acm/

• Sitio para practicar gratis: https://codeforces.com/

• Plataforma mexicana: https://omegaup.com/ (ayuda a estudiantes a participar en la OMI).

• Algoritmos y estructuras: https://cp-algorithms.com/

¿Qué opina el profesor Cormen de la programación competitiva?

Si te interesa trabajar en una gran empresa como las FANG o en casas de videojuegos AAA, es seguro que te aplicarán entrevistas técnicas -en inglés-.

Sitio para practicar gratis: https://leetcode.com/, https://www.hackerearth.com/

Investigación

Si te interesa la investigación:

• https://dl.acm.org/subject/theory

• http://www.sigact.org/

• Programa Delfín.

Historia

Recomendaciones para aprender y métodos de aprendizaje

• Programe los ejercicios en su lenguaje de programación favorito. Se recomienda Python.

• Intente resolver más ejercicios que los propuestos.

Preguntas frecuentes

¿Por qué estudiar algoritmos?

Los algoritmos son el centro de estudio de las ciencias computacionales: la algoritmia o algorítmica es la piedra angular de esta ciencia -que lo es-. Este curso tiene como propósito que tú analices algoritmos para su determinar su eficiencia, y técnicas para crearlos.

Como sabrás de tus clases de ingeniería de software, en los sistemas grandes se suele dar preferencia a:

• Modularidad,

• Corrección,

• Mantenibilidad,

• Seguridad,

• Funcionalidad,

• Tiempo de desarrollo,

• Simplicidad,

• Experiencia de usuario,

• Extensibilidad,

• Escalabilidad,

• Facilidad de leer

Entonces, ¿por qué es importante estudiar algoritmos y su rendimiento?

• El rendimiento marca la línea entre un problema factible y el que no: los seres humanos no vivimos miles de años para que un algoritmo termine.

• Algoritmos dan el lenguaje para hablar sobre el comportamiento, y no sobre cuestiones sintácticas de un lenguaje de programación. El objetivo es medir la calidad de los algoritmo por su complejidad en tiempo y espacio.

• Formalizamos algoritmos, consiguiendo crear técnicas para resolver problemas complejos: Ray Tracing, transformada de Fourier discreta, algoritmos multihilo, programación lineal, ...

Conceptos clave

Ejemplos

Latex y pseudocódigo

Tú también puedes crear algoritmos que se vean como Introduction to algorithms: https://mitp-content-server.mit.edu/books/content/sectbyfn/books_pres_0/11599/clrscode4e.pdf

Herramientas de Análisis de Algoritmos

El análisis de un algoritmo es el proceso de encontrar el tiempo y espacio necesario para ejecutarlo, abstrayendo la velocidad de ejecución de la máquina real, midiéndolo en función del tamaño y forma de la entrada.

Eficiencia (o complejidad) en tiempo y espacio

La función que mide el tiempo de ejecución de un algoritmo es $T(n)$, que relaciona el número de pasos -operaciones básicas- con el tamaño de la entrada. Por otra parte $S(n)$ mide el espacio dependiendo del tamaño de la entrada. Asumimos que trabajamos en una RAM (máquina de acceso aleatorio, la cual opera igual que una real) y que sus operaciones básicas operaciones son constantes (para mayor informacion vease un curso de arquitectura de computadoras), esto es, que no varían por el tipo ni por el tamaño de la entrada:

• Operaciones aritméticas (sumar, restar, multiplicar, dividir, resto, piso).

• Operaciones lógicas.

• Movimiento de datos (carga, copia, guardar): asignaciones.

• Control (llamadas a subrutinas, condicionales, ...).

El procedimiento para encontrar $T(n)$: contar el número de operaciones simples en función del tamaño de entrada (recurrencias, analizado amortizado, conteo, ...), luego pensar en cuales son las condiciones para que el algoritmo ejecuta la mayor, la menor y el promedio de ejecución y por último, encontrar su orden de crecimiento, esto es, su eficiencia asintótica.

El procedimiento para encontrar $S(n)$: contar el número de unidades de memoria consumidas.

Para esto es crucial que aprendas Finite Calculus.

Análisis empírico de la eficiencia de un algoritmo: «profiling» y «benchmarking»

Existen maneras empíricas o experimentales para lucidar la eficiencia de un algoritmo, sin embargo, estas no son formales, esto significa que sus resultados no son generalizables: son dependientes de la máquina, del lenguaje de programación, … Por tanto, no son objeto de estudio de este curso. Esto implica, que los ejercicios se esperan sean resueltos analíticamente: libres de un lenguaje de programación y computadoras concretas, ...

Recuerda: programar en tu lenguaje favorito y ejecutarlo para un finito casos de prueba no es una demostración.

Algunas herramientas CASE para «profiling» y «benchmarking»:

C++ Benchmark

Timeit para Python

Python profiling

JavaScript profilling

https://godbolt.org/

Tipos de tiempos de ejecución de los algoritmos

En el curso, buscamos el peor caso porque aunque el caso promedio es el típico, por la Ley de Morphy sabemos que el peor caso es siempre posible.

Caso promedio

Variables aleatorias. Es una función, X: S → N

Variables aleatorias indicadoras Es una función X: S → {1,0}

Esperanza matemática (promedio). $E[X]=\sum p_i X_i$

Distribucion uniforme. $n$ elementos, $p_i=\dfrac{1}{n}$

Ejemplos trabajados

c=1+1;  c1

b=1; c1
c= 1 if 1==b else 2;  c2

¿Cómo comparamos algoritmos?

Lo anterior significa que nuestro problema de comparar algoritmos se reduce a comparar funciones $T_1,T_2$, tal que si

El algoritmo con $T_2$ es más rápida que el algoritmo con $T_1$, donde siempre se quiere la función más pequeña -más cercana a 0-, por tener menor tiempo de ejecución.

Ejemplo 1

• Si $T_1(n)=n$ y $T_2(n)=1$ ¿Cuándo $T_1(n) \ge T_2(n)$?

  $T_1(n)=n$

  $T_2(n)=1$

  $$n \ge1, \text{para alguna } n_0$$

  https://www.geogebra.org/calculator/mkk7dpeq

  https://www.geogebra.org/calculator/mkk7dpeq

  ¿En cuáles $n$ dos funciones se intersecan o son iguales?

  $$T_1(n)=T_2(n)\\ n_0=1$$

Ejemplo 2

• Supón que estamos comparando implementaciones de insertion sort y merge sort en la misma máquina. Para entradas de $n$, insertion sort corre en $8n^2$ pasos, mientras que merge sort corre en $64nlg(n)$ pasos. ¿Para cuáles valores de $n$, insertion sort supera a merge sort?

  $\text{¿Para cuáles }8n^2 \text{ es más rápida } 64nlg(n)?$ Esto implica

  $$8n^2<64nlg(n)\\ 8n^2<64n\dfrac{ln(n)}{ln(2)}\\ nln(2)<8ln(n)\\ \dfrac{ln(2)}{8}<\dfrac{ln(n)}{n}\\ \dfrac{ln(2)}{8}<\dfrac{ln(n)}{e^{ln(n)}}\\ \dfrac{log(2)}{8}<ln(n)e^{-ln(n)}\\ -\dfrac{log(2)}{8}>-ln(n)e^{-ln(n)}\\ -ln(n)>W_(\dfrac{-log(2)}{8})\\ n<e^{-W(\dfrac{-log(2)}{8})}\\ e^{-W_{-1}(\dfrac{-log(2)}{8})}<n<e^{-W_{0}(\dfrac{-log(2)}{8})}\\$$

  https://www.geogebra.org/calculator/g7axrebz

Ejemplo 3

• ¿Cuál es el valor más pequeño tal que un algoritmo cuyo tiempo de rendimiento es $100n^2$ es más rápido que un algoritmo de tiempo $2^n$ en la misma máquina?

  $$100n^2=2^n\\ \dfrac{100n^2}{2^n}=1\\ \dfrac{n^2}{e^{ln(2^n)}}=\dfrac{1}{100}\\ \dfrac{n^2}{e^{nln(2)}}=\dfrac{1}{100}\\ n^2e^{-nln(2)}=\dfrac{1}{100}\\ ne^{-nln(2)/2}=\dfrac{1}{10}\\ \dfrac{-nln(2)}{2}e^{\dfrac{-nln(2)}{2}}=\dfrac{-ln(2)}{20}\\ W(\dfrac{-ln(2)}{20})=\dfrac{-nln(2)}{2}\\ n=\dfrac{-2W(\dfrac{-ln(2)}{20})}{ln(2)}=\{0,15\}\\ sup(n)=15\\ \text{ desde } 15 \text{ a } \infty \text{, }100n^2<2^n$$

Ejemplo 4

• Determine la $n$ más grande que $f(n)=log_2(n)=lg(n)$ que pueda resolver en 1 segundo, suponiendo $f(n)$ toma $lg(n)$ microsegundos.

  $$\dfrac{f(n)}{operaciones} \le 1 \text{ s =}10^6 \mu s$$

  $$f(n)\le(10^6\times operaciones) \text{ instrucciones }$$

  $$lg(n)=(10^6\times o) ,n=2^{10^6\times o}$$

  Donde $operaciones=o$, medida en $instrucciones/tiempo$, indica cuántas instrucciones se ejecutan por unidad de tiempo, en el ejemplo, $o= 1\mu s$

  $$n=2^{10^6}$$

¿Cómo demostramos que un algoritmo/programa funciona? Program verification and correctness

Manual

Cálculo de predicados, condiciones débiles (precondiciones) y fuertes postcondiciones -Predicate transformer semantics, Hoare logic-

https://raw.githubusercontent.com/fraunhoferfokus/acsl-by-example/master/ACSL-by-Example.pdf

https://allan-blanchard.fr/publis/frama-c-wp-tutorial-en.pdf

Invariante de lazo. Cálculo particular de Hoare Logic para ciclos.

T g() {}
// Si inicie bien -Inicialización. Establecimiento. Precondiciones- y
Q;
// me mantego haciendolo bien -Mantenimiento. Preservación.-
// Invariente I
while(P(Q)) {
   // Q --> no P(Q)
}
// cuando terminé -Terminación.-
assert no P(Q) and I;

// estaré bien.
}

Ejemplo:

int f() {
   // Si inicie bien -Inicialización. Establecimiento. Precondiciones- y
   int i = 0;
   // me mantego haciendolo bien -Mantenimiento. Preservación.-
   //@ loop invariant 0 <= x <= 30
   while(i < 30) {
        i++;
   }
   // cuando terminé -Terminación.-
   //@ assert i == 30; // por que [no (i < 30) y (0 <= i <= 30)]
   // estaré bien.
   return i;
}

Máquina de estados.

Automática

Lean Prover.

COQ.

WhyML

FramaC.

Why3.

https://sanchezcarlosjr.medium.com/state-of-art-in-correctness-made-by-compilers-4b89f964d29

https://www.adacore.com/uploads/technical-papers/2016-10-SPARK-MisraC-FramaC.pdf

Algunos shortcircuits

if (P)
   if (Q)
      r;

es equivalente

if (P && Q)
   R;

Referencias

Tony Hoare’s paper, “An Axiomatic Basis for Computer Programming”.

https://cacm.acm.org/magazines/2015/4/184701-how-amazon-web-services-uses-formal-methods/fulltext

https://raw.githubusercontent.com/blanchette/logical_verification_2021/main/hitchhikers_guide.pdf

https://www.youtube.com/watch?v=U5i2VQj5jPk&ab_channel=Computerphile

https://www.youtube.com/watch?v=WwOVmvSQu2w&list=PLL1cieOZqlW4EI43XJkKeYobDGsmXtZEM&index=6&ab_channel=smm_oficial

https://www.quora.com/Why-did-Dijkstra-say-that-“Object-oriented-programming-is-an-exceptionally-bad-idea-which-could-only-have-originated-in-California-”

Caso de estudio: suma

Input: Una secuencia de $n$ números reales $[a_1,a_2,a_3,...,a_n]$.

Output: Un valor real $r$, tal que $r=\sum_i^n a_i$

SUM(A)
	n = A.length                 c1(1)
  r = A[n]                     c2(1)        
	for j = n-1  downto 1        c3(n)
	     do r = r + A[j]         c4(n-1)
	return r                     c5(1)

Invariante de lazo. En el inicio de cada iteración del bucle for lineas 3-4, $r$ es igual a la suma de los $n-j$ últimos elementos de $A$.

• Inicialización.

  Al inicio de la primera iteración, $j=n-1$ y $r=a_n$, por lo tanto $r$ es igual a la suma de los $n-(n-1)=1$ últimos elementos de $A$, lo cual implica que se cumple la invariante de lazo.

• Mantenimiento.

  Al inicio de la iteración donde $j=k$, suponemos cierta la invariante por lo que $r=a_n+a_{n-1}+a_{n-2}+...+a_{n-k}$ (la suma de los $n-j$ últimos elementos de $A$). En la línea $4$, el elemento $A[j]=A[k]$ es sumado a $r$, i.e., al inicio de la siguiente iteración, donde $j=k-1$, $r=a_n+a_{n-1}+a_{n-2}+...+a_{n-k}+a_{n-(k-1)}$ es decir, la suma de los $n-(k-1)=n-k+1$ últimos elementos de $A$, lo cual implica que se cumple la invariante de lazo.

• Finalización.

  Cuando el bucle termina, $j=n$, y por la invariante tenemos $r=a_n+a_{n-1}+a_{n-2}+...+a_{n-k}+a_{n-(k+1)}+...+a_1$, es decir que contiene la suma de los y tenemos que $n-j=n-0=n$ últimos elementos de $A$ (i.e., la suma de todos los elementos de $A$).

Por lo tanto, el algoritmo es correcto.

Complejidad temporal.

$T(n)=c_1+c_2+c_3n+c_4(n-1)+c_5=(c_3+c_4)n+(c_1+c_2-c_4+c_5)$.

Caso de estudio: búsqueda binaria

Entrada: Una secuencia de n números A = <a1, a2,..., an> y un valor v.

Salida: Un índice i tal que $v = A[i]$ o el valor especial NIL si v no se encuentra en A.

binary_search(A, v):
  if A[-1] < v:
    return Nil
  p = 0
  r = len(X)
  while p < r:
    mid = (p+r)//2
    if A[mid] == v:
      return mid
    if A[mid] < v:
       p = mid + 1
    if A[mid] > v:
       r = mid - 1 
  return Nil

• Utilizando la técnica de invariante de lazo, demuestre que el algoritmo es correcto.

• Calcule el tiempo de ejecución $T(n)$ en el mejor y peor caso. Calcule también el total en promedio, suponiendo que el elemento a buscar es cualquiera de los contenidos en el vector con la misma probabilidad. Exprese los casos utilizando notación asintótica.

Notebook

Notas y recursos

Para visualizar alguno de los algoritmos: https://visualgo.net/en o https://algorithm-visualizer.org/

https://tildesites.bowdoin.edu/~ltoma/teaching/cs231/duke_cps130/Lectures/L06.pdf

https://www.cs.stanford.edu/~trevisan/cs254-10/lecture02.pdf

https://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/19/Small19.pdf

Preguntas frecuentes y no tan frecuentes

¿Hay $\theta$ (theta pequeña)?

No. https://stackoverflow.com/questions/25593619/why-doesnt-small-theta-asymtotic-notation-exist

¿Es lo mismo peor caso, mejor caso y caso promedio que el análisis asintótico?

No.

Técnicas de Diseño de Algoritmos

La siguiente lista -no exhaustiva- de técnicas, patrones de diseño, métodos o paradigmas son enfoques para encontrar algoritmos óptimos:

• Divide y vencerás

• Programación dinámica

• Estrategias voraces

• Métodos probabilístico o algoritmos aleatorios

• Algoritmos de aproximación

• Métodos Heurísticos.

• Backtracking.

• Ramificación y poda (Branch and Bound).

• Fuerza bruta (búsqueda exhaustiva).

Divide y vencerás (divide et impera)

Para resolver problemas con Divide y vencerás consiste en los siguientes tres pasos:

• Divide el problema en subproblemas substancialmente más pequeños e independientes.

• Resuelve los subproblemas recursivamente cuando sean grandes (caso recursivo), pero si el tamaño del sub-problema es suficientemente pequeño simplemente resuélvelo (caso base).

• Combina las soluciones de los subproblemas en la solución del problema original.

Análisis

Los algoritmos recursivos deben analizarse de manera distintos a otra clase: usamos recurrencias, porque son una manera natural de medir su tiempo.

Relaciones de recurrencia

Dos maneras de resolver la recurrencia:

• Árbol de recurrencias.

• Ecuaciones de recurrencia.

• Método maestro: $T(n)=aT(n/b)+f(n)$, $a\ge1, b>0$.

  Si $f(n)=\Theta(n^{log_b(a)})$ entonces $T(n)=\Theta(n^{log_ba}lg(n))$

  Si $f(n)=\Omega(n^{log_ba+\epsilon})$ para alguna constante $\epsilon>0$ y $af(n/b)\le cf(n)$ para alguna constante $c<1$ y todas las $n$ suficientemente grandes, entonces $T(n)=\Theta(f(n))$.

  Si $f(n)=O(n^{log_b(a)-\epsilon})$ para alguna constante $\epsilon>0$, entonces $T(n)=\Theta(n^{log_ba})$

Sin embargo, como te darás cuenta en los siguientes ejercicios, el método maestro, aunque bastante rápido, es bastante limitado, asi surgio la necesidad de generalizarlo: método Akra–Bazzi (https://link.springer.com/article/10.1023/A:1018373005182.

Una manera de demostrar nuestra suposición:

• Método de sustitución.

Ejemplo 1 con Árbol de recurrencias.

Sum(n) {
    if n == 1
        return 11
    return n + Sum(n-1)
}

• Solución

  $T(n)=T(n-1)+O(1)=O(n)$

  

Ejemplo 2 con Método maestro

recursiveFun1(n)
{
    if (n <= 0)
        return 11;
    else
        return 11 + recursiveFun1(n/2);
}

• Solución

  $T(n)=aT(n/b)+f(n)=T(n/2)+c=\Theta(lg(n)),a=1,b=2$

  1.

  $f(n)=O(n^{log_2(1)-\epsilon})\\ cn^0 =O(n^{log_2(1)-\epsilon})$, $log_2(1)-\epsilon=0$, $\epsilon=-log_2(1)=0$

  2.

  $f(n)=\Theta(n^{log_2(1)})\\ cn^0 =\Theta(n^{log_2(1)})$, $0=log2(1)$

  $T(n)=\Theta(n^{log_2(1)}lg(n))=\Theta(lg(n))$

Ejemplo 3 con Método maestro

recursiveFun3(n)
{
    if n <= 0
        return 11
    else
        return 11 + recursiveFun3(n/5)
}

• Solución

  1.

  $f(n)=O(n^{log_5(1)-\epsilon})\\ cn^0 =O(n^{log_5(1)-\epsilon})$,

  $log_5(1)-\epsilon=0$, $\epsilon=-log_5(1)=0$

  2.

  $f(n)=\Theta(n^{log_5(1)})\\ cn^0 =\Theta(n^{log_5(1)})$, $0=log5(1)$

  $T(n)=\Theta(n^{log_5(1)}lg(n))=\Theta(lg(n))$

  Entonces $T(n)=\Theta(lg(n))$

Ejemplo 4

int recursiveFun2(int n)
{
    if (n <= 0)
        return 11;
    else
        return 11 + recursiveFun2(n-5);
}

• Solución

  $T(n)=c,n\le0$

  $T(n)=T(n-5)+c,n\ge1$

  $i=\lceil\dfrac{n}{5}\rceil+1$

  $T(n)=(\lceil\dfrac{n}{5}\rceil+1)c=\lceil\dfrac{n}{5}\rceil c+c\le cn+c= O(n)$

Ejemplo 5

int recursiveFun5(int n)
{
    for (i = 0; i < n; i += 2) {
        // T(n)=c1+c2+c3+...=c
    }
    if n <= 0
        return 1
    else
        return 1 + recursiveFun5(n-5)
}

• Solución

  $T(n)=c_1,n\le0$

  $f(n)=c_2\lceil\dfrac{n}{2}\rceil +c_3$

  $T(n)=T(n-5)+f(n),n\ge1$

  $i=\lceil\dfrac{n}{5}\rceil+1$

  $T(n)=(\lceil\dfrac{n}{5}\rceil+1)(c_2\lceil\dfrac{n}{2}\rceil +c_3)\le c_2n^2+c_1n+c_3=O(n^2)$

Ejemplo 6

void recursiveFun4(int n, int m, int o)
{
    if (n <= 0)
    {
        printf("%d, %d\n",m, o);
    }
    else
    {
        recursiveFun4(n-1, m+1, o);
        recursiveFun4(n-1, m, o+1);
    }
}

• Solución

  Dado que la cantidad de pasos esta determinada por $n$, entonces:

  • printf es constante.

  • Buscamos $T(n)$

  Así

  $T(n)=2T(n-1)+O(1)=(2^{n+1}-1)c_1=\Theta(2^n)$

Ejemplo 7 Factorial

factorial(n)
{
    if (n == 0)
    {
        return 1
    }
    return n * factorial(n-1);
}

• Solución

  $T(n)=T(n-1)+c$

  $T(n-1)=T(n-2)+c$

  ...

  $T(1)=T(0)+c$

  $T(0)=c$

  $T(n)=(n+1)c=cn+c$

Caso de estudio: Permutación

Encuentra $T(n)$, $\Omega(n)$ para cualquier algoritmo de permutación y elimina la recursión.

string permute(string str, int index = 0, string acc = "") {
    if (index == str.length() - 1) {
        acc += str + "\n";
        return acc;
    }
    for (int subIndex = index; subIndex < str.length(); subIndex++) {
        swap(str[index], str[subIndex]);
        acc = permute(str, index + 1, acc);
    }
    return acc;
}

• Solución

  $T(n)=O(n!)$

  permute(elements):
      x = elements
      y = []
      n = len(x)-1
      while n > 0:
        for i in range(0, len(x), n+1):
          for j in range(i, i+n+1):
            for k in range(i, i+n+1):
              if j != k:
                  y.append(x[j]+x[k][-1])
        n = n-1
        x = y
        y = []
      return x

Caso de estudio: Máximo común divisor

Encuentra $T(n)$ y elimina la recursión.

gcd(int a, int b)
  if b == 0
     return a
  return gcd(b, a mod b)

• Solución

  gcd(int a,int b)
    while b != 0
      a,b = b, a mod b
    return a

Los problemas, mas no las soluciones, fueron obtenidos en

https://stackoverflow.com/questions/13467674/determining-complexity-for-recursive-functions-big-o-notation

https://github.com/sanchezcarlosjr/uabc/blob/main/src/datastructure-week5-test/PermutationAlgorithm.h

Programación dinámica (PD)

Creada por Richard Bellman en la RAND corporation, programación es, por inglés británico, optimización. Proviene de programación lineal -método tabular- y no refiere a escribir código. El nombre puede ser un poco oscuro, y eso es por cuestiones políticas: el nombre fue eligido para convencer a sus jefes ocultando el hecho de que estaban investigando matemáticas, programación porque estaba de moda y dinámico para que el nombre suene más interesante. El nombre original era: optimally plan multistage processes.

Esta técnica es parecida a divide y vencerás, donde en aquel vimos subproblemas independientes y pequeños ($n/b$) resueltos recursivamente, en programación dinámica los subproblemas son dependientes, no tan pequeños ($n-a$), resueltos iterativamente, y regularmente usado para problemas de optimización (lo cual implica tomar decisiones dirigida a encontrar la mejor solución). En general, convierte algoritmos con tiempo exponencial a tiempo polinomial.

Este paradigma resuelve cada subsubproblema y entonces lo guarda en una tabla, evitando el recálculo cuando los siguientes subproblemas necesiten la respuesta a ese subsubproblema, a esto se le conoce como memoización (no memorizar, memoizar), que es la idea central de PD, que en otras palabras, memoizar significa recordar y reusar soluciones de subproblemas.

Pasos para usar este paradigma:

1. Caracterizar la estructura de una solución óptima.

2. Definir recursivamente el valor de una solución óptima.

3. Calcular el valor de una solución óptima en un esquema bottom-up (iterativo) o top-down (recursivo).

4. Construir una solución óptima a partir de la información calculada.

O también puedes el marco de trabajo SRBOT:

1. Definir subproblema con palabras.

2. Relacionar las soluciones de los subproblema recursivamente.

3. Orden topológico de los subproblemas (en este caso, es un subproblema DAG).

4. Caso base de la relación.

5. Original problema vía subproblemas.

6. Tiempo de análisis.

Notas y referencias

MIT 6.006 Introduction to Algorithms, Spring 2020

MIT 6.006 Introduction to Algorithms, Fall 2011

Estrategias voraces, ávidas o glotonas (Greedy algorithms)

Al igual que la programación dinámica, los algoritmos voraces buscan una solución con el óptimo resultado, en el primero para algunos problemas determinar la mejor solución global dado el conjunto de pasos en cada paso puede ser muy costoso, en el segundo buscamos la mejor solución en el momento, esto significa, seleccionar soluciones óptimas locales repetidamente con esperanza de que esa sea la solución global, claramente, esto no significa que no siempre dará la solución óptima global.

Pasos para usar este paradigma:

1. Caracterizar la subestructura óptima del problema.

2. Desarrollar una solución recursiva.

3. Mostrar que la elección es voraz, entonces un subproblema pertenece.

4. Demostrar que es una elección segura.

5. Desarrollar un algoritmo recursivo que implemente la estrategia voraz.

6. Convertir el algoritmo recursivo a uno iterativo.

Notas y referencias

Campos, J. (2021). Algoritmos voraces. Universidad de Zaragoza. http://webdiis.unizar.es/asignaturas/AB/material/2-Algoritmos Voraces.pdf

Métodos probabilísticos -Algoritmos aleatorios-

Si un algoritmo, que además de su entrada, usa un generador de números aleatorios o toma decisiones aleatorias en su ejecución, entonces es aleatorio, cuando solo depende de su entrada es determinista. En la práctica, usamos generadores pseudoaleatorios. El tiempo de ejecución y, en otros casos su salida, no son fijos para una entrada dada.

Ejemplos

Ejemplo 1 Algoritmos de Las Vegas (LV)

Entrada. Una secuencia de n elementos $a_0,a_1,...,a_n$, el elemento $a$ y $a$ pertenece a la sequencia.

Salida. $i$ tal que $a=a_i$.

buscar_el_elemento(a, A)
 i = 0
 while A[i] != a
    i = RANDOM(0, A.length) #  0 <= i <= A.length, i es aleatorio
 return i

Ejemplo 2 Algoritmos de Monte Carlo (MC)

Entrada. Una secuencia de n elementos $a_0,a_1,...,a_n$, el elemento $a$ y $k$ el límite de iteraciones.

Salida. $i$ tal que $a=a_i$.

buscar_el_elemento(a, A, k)
   for i=0 to k
      j=RANDOM(0, A.length) #  0 <= j <= A.length, j es aleatorio
      if A[j] == a
         return j

Notas y referencias

Karp, R. M. (1991). An introduction to randomized algorithms. Discrete Applied Mathematics, 34(1-3), 165-201.

Wootters, M. (2022, May 17). Class 1, Video 1: Introduction. Youtube. Retrieved from https://www.youtube.com/watch?v=01ohO542NMI&list=PLkvhuSoxwjI_JL7GYcJHK7-EK55t0KYGO&ab_channel=MaryWootters

Algoritmos de aproximación

Una amplia variedad de problemas importantes son NP-completos (horario de trabajo, el problema del viajero o vendedor, ...), entonces no podemos sencillamente abandonarlos porque no sabemos algoritmos que lo resuelvan en tiempo polinomial. Para esto, diseñamos algoritmos con tiempo polinómico que se acercan a la solución por un factor: radio de aproximación $\rho(n)$ tal que

donde $C^*$ es el costo de la solución óptima y $C$ es el costo de producido por el algoritmo. Algunos tambien a estos algoritmos heúristicos.

Corutinas

Co-routines as an alternative to state machines - Eli Bendersky's website. (2022, September 17). Retrieved from https://eli.thegreenplace.net/2009/08/29/co-routines-as-an-alternative-to-state-machines

Recursión mutua

Tail call

Máquinas de estado

Iteradores

Generadores

Stream (pattern observer)

Preguntas frecuentes

¿Todos los algoritmos recursivos siguen un enfoque divide y vencerás?

No.

¿Estas técnicas son mutuamente excluyentes, esto es, si puedo aplicar una, no puedo aplicar las otras?

Son mutuamente excluyentes.

La RAE no recoge el verbo memoizar ni la memoización, debe ser memorizar y memorización

Notebook

Algoritmos sobre grafos

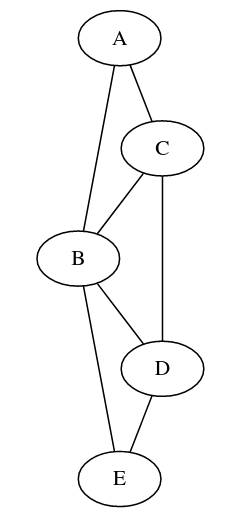
Representación o ¿qué estructura de grafos usamos?

{
  "A": {"B", "C"},
  "B": {"A", "C", "D", "E"},
  "C": {"A", "B", "D"},
  "D": {"C", "B", "E"},
  "E": {"D", "B"}
}

def solve(s)
	if s is solution
	  yield s
	for x in s
	   yield from solve(x)

Elementales

Maneras de atrevesar un árbol:

• In-order traversal (LVR)

• Reverse order traversal (RVL)

• Preorder traversal (VLR) -DFS-

• Postorder traversal (LRV)

• Normal Level Order Traversal -BFS-

BFS

BFS es un algoritmo que recorre todos los hijos de un nodo A y continua con sus hijos.

frontier = Queue()
visited = {}
while frontier is not empty:
    node = frontier.pop()
    if node not in visited:
        visited.add(node)
        for each child of node's children:
            node.relax(child)
            frontier.push(child)
return failed

DFS

Depth-first search, también llamado Backtracking [1], Euler tour o recorrido en orden si es un árbol, es un algoritmo que recorre el nodo más profundo, regresa al primero de la pila (el padre) y continua con el siguiente nodo. Este algoritmo suele ser presentado en su forma recursiva, porque así se ahorra implementarlo, esto es, sustuimos nuestra pila por la pila de recursividad.Tg

PseudoDFS

frontier = Stack()
visited = {}
while frontier is not empty:
    node = frontier.pop()
    if node not in visited:
        visited.add(node)
        for each child of node's children:
            node.relax(child)
            frontier.push(child)
return failed

• Convierte el DFS a una versión iterativa usando pilas.

  class DepthFirstSearcher:
    def __init__(self, graph):
      self.graph = graph
      self.records = set()
    def explore(self):
      found = False
      for vertex in self.graph.vertices():
         if vertex not in self.records:
            found, v = self.visit(vertex)
            if found:
               return found, v 
    def visit(self, vertex):
       stack = []
       v = vertex
       while True:
         pivot = v
         while v != None:
            while v != None and v not in self.records:
              stack.append(v)
              self.records.add(v)
              if len(stack) >= 2:
                self.graph.setEdge(stack[-2], stack[-1])
              if self.graph.isAGoal(v):
                return True, v
              pivot = v
              v = self.graph.exploreNeighbor(v)
            v = self.graph.exploreNeighbor(pivot)
         stack.pop()
         self.graph.finish(v)
         if len(stack) == 0:
            return False, None
         v=self.graph.exploreNeighbor(stack[-1])

  💡

  Otra solución es un pseudo DFS que cambia una cola a una pila en el algoritmo BFS. https://stackoverflow.com/questions/20429310/why-is-depth-first-search-claimed-to-be-space-efficient

Algoritmo

Note que si realizamos una evaluación al nodos para obtener una solución es un problema de búsqueda.

frontier = Frontier()
visited = {}
while frontier is not empty:
    node = frontier.pop()
    if isGoal(node):
        return path_to_node
    if node not in visited:
        visited.add(node)
        for each child of node's children:
            node.relax(child)
            frontier.push(child)
return failed

DAG

DAG aplicaciones

Merkle DAGs. IPFS, Git, … Content linking via directed acyclic graphs (DAGs).

Topological Sorting

Aplicaciones

Si necesitar calenderizar con requisitos, Topological Sorting tiene sentido. Aunque más generalmente, Feedback arc set.

Makefile

a: b c
	@echo "A"
b: c
	@echo "B"
c:
  @echo "C"

Al ejecutar make obtenemos

C
B
A

¿Por qué? Dibujemos el grafo:

graph TD
  C --> B
  C --> A
  B --> A

Ejecute el Topological Sorting.

Pruebe con la utilidad de Unix: tsort.

Revisar la Herencia orientado a objetos.

Revisión y ejecución de Dependencias.

Notebook

Laberinto

Crea tus propios algoritmos para conseguir ir del punto A al punto B en un un laberinto.

https://graph-theory.sanchezcarlosjr.com/

Notas y referencias

[1] https://arxiv.org/pdf/cs/0011047.pdf. En esto puede llegar a existir confusión.

Preguntas frecuentes

¿Existe un compendio de todos los teoremas, definiciones, ...?

https://people.math.sc.edu/cooper/math776/StudyGuide.pdf

¿Red o grafo?

Grafo es el concepto abstracto matemático.

Red es el grafo que representa objetos del mundo real, los nodos son entidades del sistema y las aristas representan la relacion entre ellos.

Sin embargo, en la literatura puedes encontrarlos indistintamente.

https://bence.ferdinandy.com/2018/05/27/whats-the-difference-between-a-graph-and-a-network/

https://arxiv.org/pdf/1302.4378.pdf

http://networksciencebook.com/

¿Existen base de datos que guarden grafos?

Sí, este tipo de base de datos ya tienen integrados los algoritmos vistos aquí. .

Notas y referencias

Para aprender de manera visual teoría de grafos: https://d3gt.com/unit.html, usar el apéndice de CLRS, o el libro Frank Harary. Graph Theory. Addison-Wesley, 1969.

Ensayo sobre la representación de grafos: https://www.python.org/doc/essays/graphs/

Network Time Protocol

Introducción a la Teoría de la Computación

Complejidad computacional

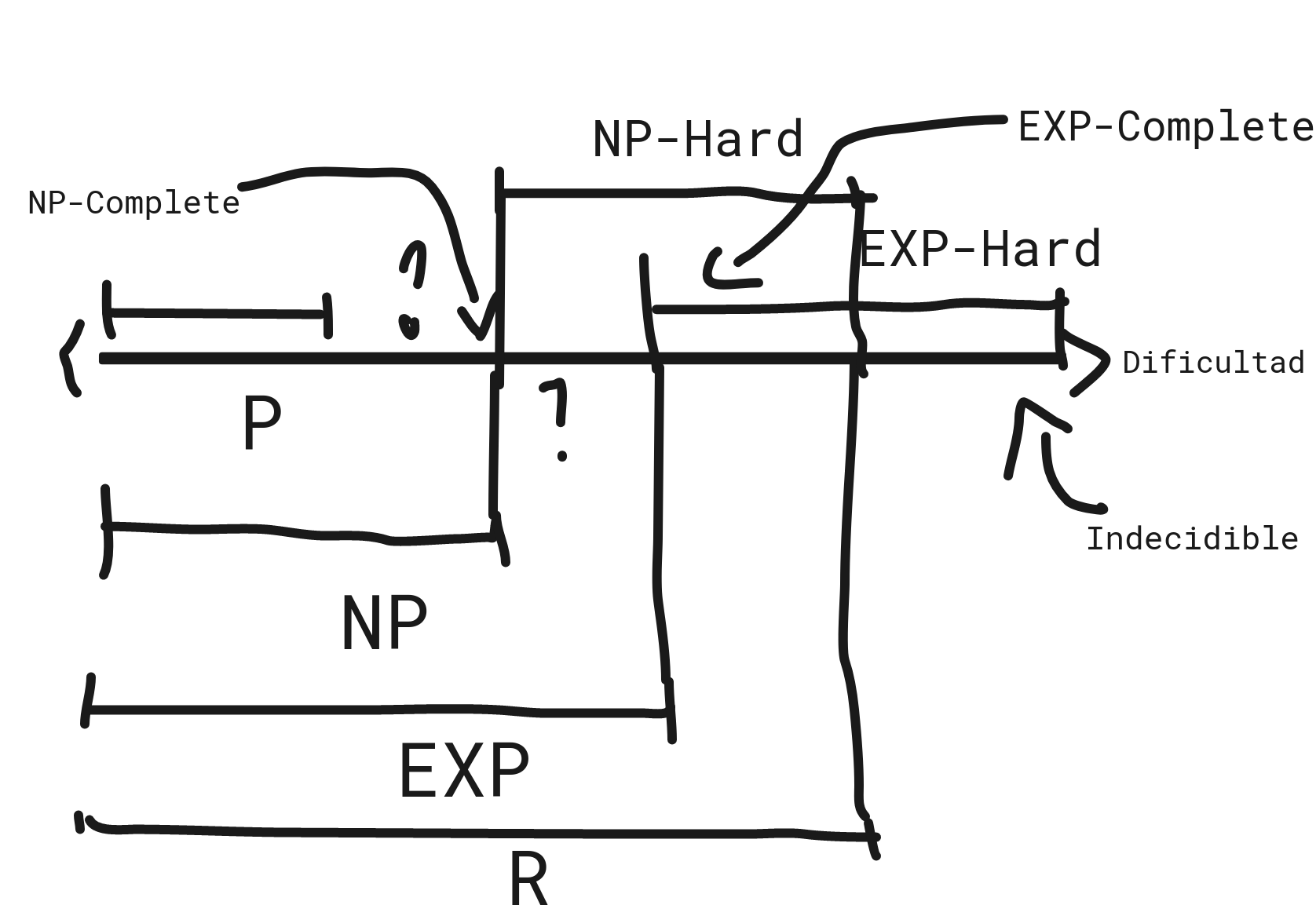
SAT

Aplicaciones

Sodoku.

Teorema Cook-Levin

Notas y referencias

https://plato.stanford.edu/entries/computational-complexity/

¿Qué es lo que sigue? ¿Cuál es el estado del arte?

Algoritmos heúristicos

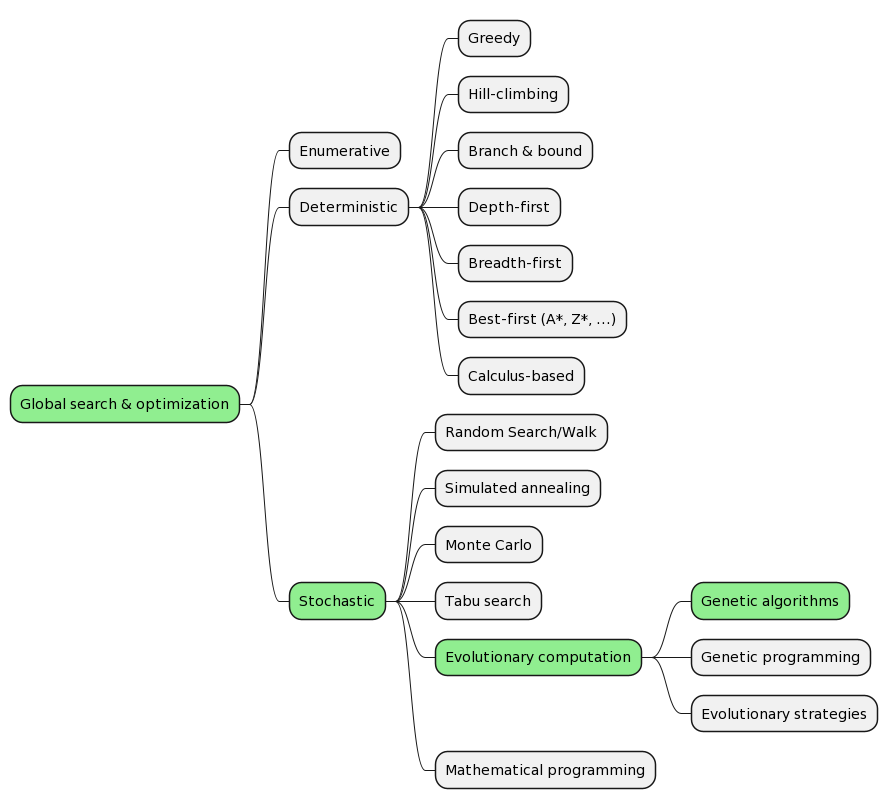
Algoritmos paralelos

Hilos y procesos hijo.

Model Actor

Async

Geometria computacional

MapReduce

Algoritmos cuánticos

Operaciones asíncronas

Sincronas.

Asincronas.

Diseño de sistemas

Distributed hash table