The Gauss idea is to solve AA^-1 = I. finding each column of A^-1:

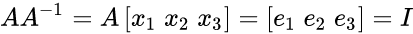
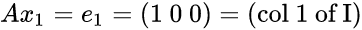
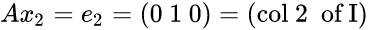
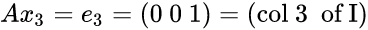
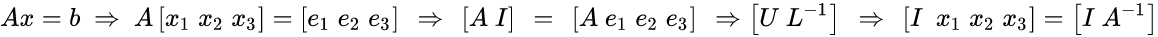
Worked example

Prove PT=P−1\text{Prove } P^T = P^{-1}
PP−1=IPP^{-1}=I
Px1=(100)Px_1 = \begin{pmatrix} 1 & 0 & 0 \end{pmatrix}
(Row 1 of P)∗x1=1\text{(Row 1 of P)}*x_1=1
(Row n of P)∗x1=0\text{(Row n of P)}*x_1=0
P[...x1...]=[100...]P\begin{bmatrix} ...\\ x_1 \\ ...\end{bmatrix}=\begin{bmatrix} 1\\ 0 \\0 \\... \end{bmatrix}
[...1...]∗[...a...]=1 where ... are 0\begin{bmatrix} ... & 1 & ... \end{bmatrix}*\begin{bmatrix} ...\\ a \\... \end{bmatrix}=1 \text{ where ... are 0}
 such that 0∗0+0∗0+...+1∗a+0∗0...=1,a=1\text{ such that } 0*0+0*0+...+1*a+0*0...=1,a=1
(Row i of P)=xiT\text{(Row i of P)}=x_i^T
[Row1Row2...]=[x1Tx2T...]\begin{bmatrix} Row1\\ Row2 \\ ...\end{bmatrix}=\begin{bmatrix} x_1^T\\ x^T_2 \\ ...\end{bmatrix}
We have[Row1Row2...][x1x2...]=[P][...x1...]+...=[100010001]=I\text{We have} \begin{bmatrix} Row1\\ Row2 \\ ...\end{bmatrix}\begin{bmatrix} x_1 & x_2 ... \end{bmatrix}=\begin{bmatrix} P \end{bmatrix} \begin{bmatrix} ...\\ x_1 \\ ...\end{bmatrix}+...=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 &0 \\ 0 & 0&1\end{bmatrix}=I
PPT=I,PT=P−1 Q.E.DPP^{T}=I, P^T=P^{-1} \text{ Q.E.D}