Physics
Resources
Course of Theoretical Physics
Lev Landau (Vol. 1–3, 5–8) Evgeny Lifshitz (Vol. 1–10) Vladimir Berestetskii (Vol. 4) Lev Pitaevskii (Vol. 4, 9–10)
Units
Billon is in English, Portuguese, and Greek -"Mil millones" in Spanish. But, It's in Spanish -trillion in English.
Motion
1. , falta el desplazamiento ()
2. , falta la aceleracion
3. , falta v
4. , falta t
Kinetic and Static Friction
| Key points |
|---|
| Two objects are moving relative to each other. |
| Two surfaces are non-moving but there is still a lateral force. If F>Fs then object start to move. |
Example 1.
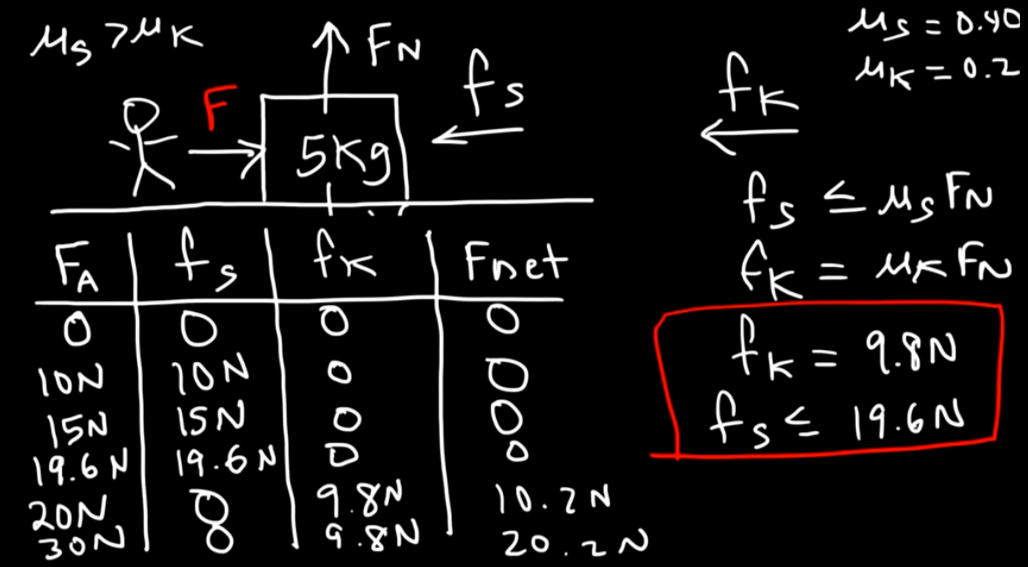
| Typical surface | Coefficient of static friction | Coefficient of kinematic friction |
|---|---|---|
| Wood | 0.25 - 0.5 | 0.2 |
| Glass | 0.4 - 1 | 0.4 |
| Steel | 0.2 | 0.6 |
| Rubber | 1 | 0.8 |
| Teflon | 0.04 | 0.04 |
Circular Motion Dynamics
Resistive forces
When a solid object moves through a fluid (liquid or gas) it will experience a resistive force, called the drag force, opposing its motion. This force depends on both the properties of the object and the properties of the fluid. It also depends on the the density, viscosity, and compressibility of the fluid.
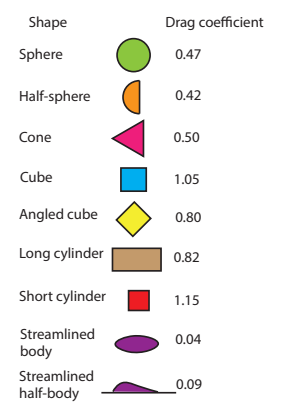
| The Coefficient C is called the drag coefficient. |
|---|
| The cross-sectional area A of the object in a plane perpendicular to the motion. |
| The resistive force is roughly proportional to the square of the speed V. |
| The density P of the air. |
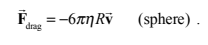
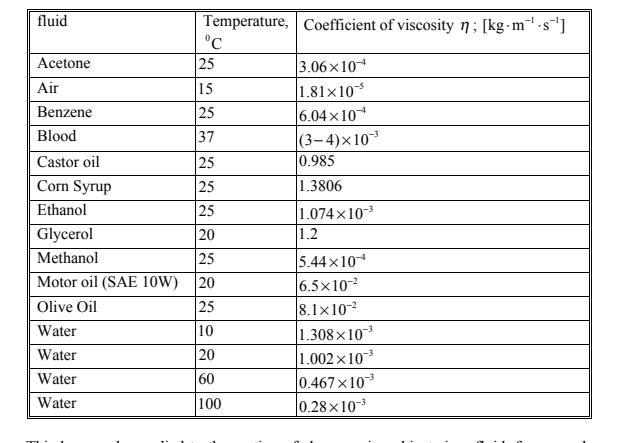
Resistive forces - low speed case
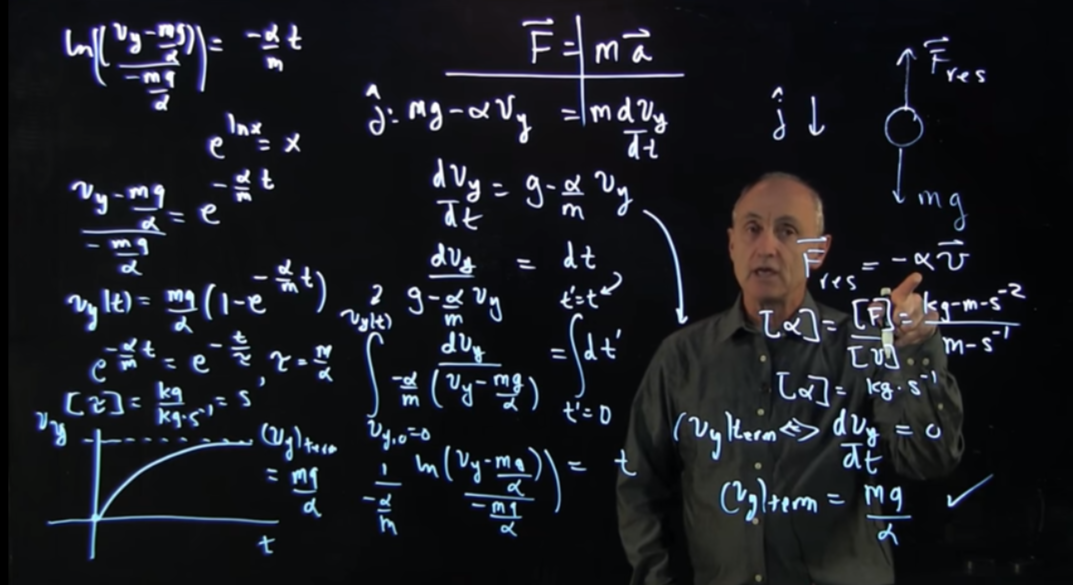
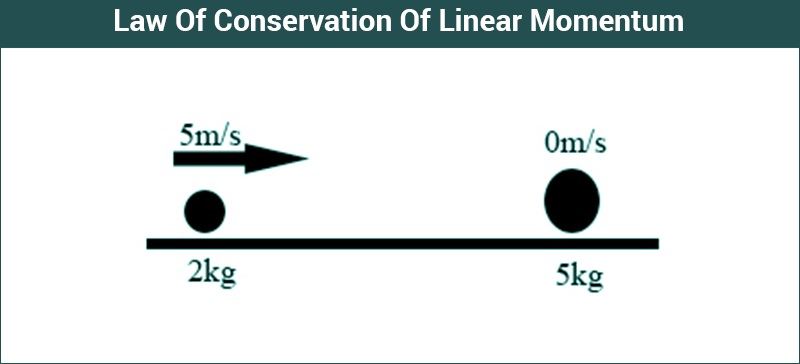
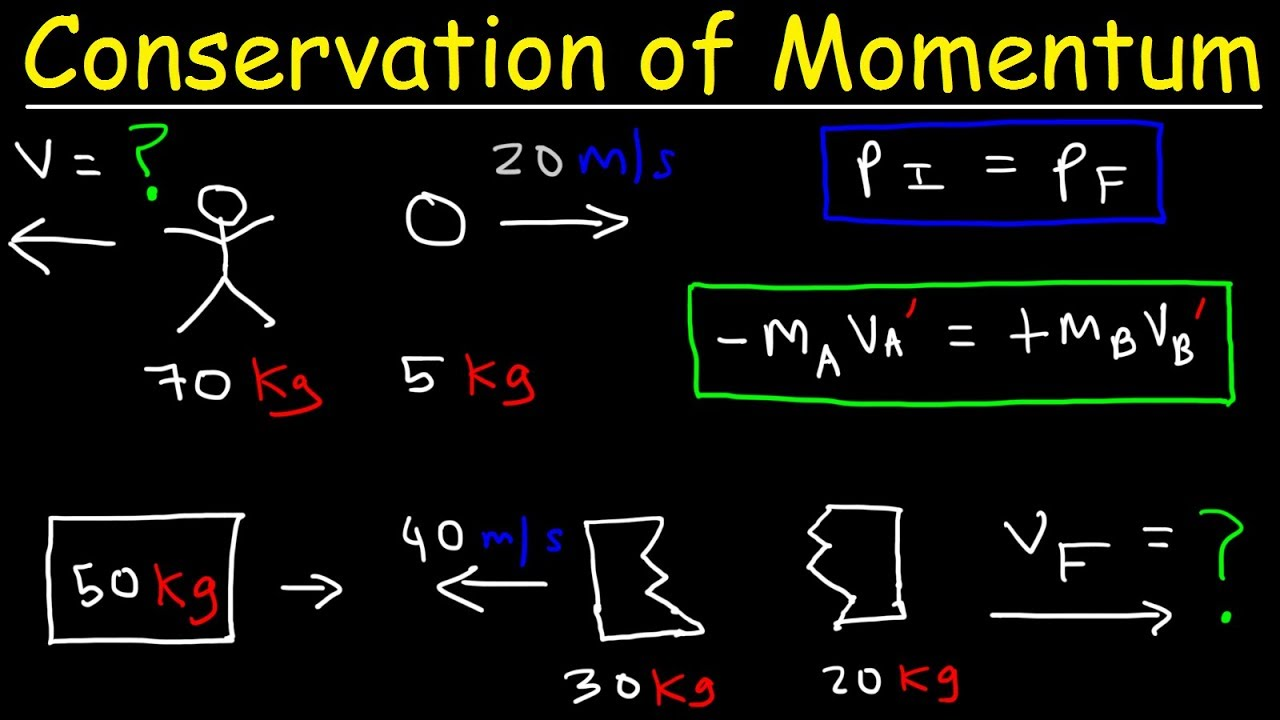
Linear momentum
Linear momentum is a vector quantity, product of an object's mass and velocity. Also called “momentum” for short. Momentum describes the amount of mass in motion.

How momentum and net force are related
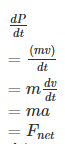
Forces cause a change in momentum, but momentum does not cause a force. The bigger the change in momentum, the more force you need to apply to get that change in momentum.
Impulse
Impulse (symbolized by J or Imp) is the integral of a force, F, over the time interval, t, for which it acts. Since force is a vector quantity, impulse is also a vector quantity. Impulse applied to an object produces an equivalent vector change in its linear momentum, also in the same direction.
Angular force
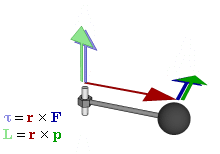
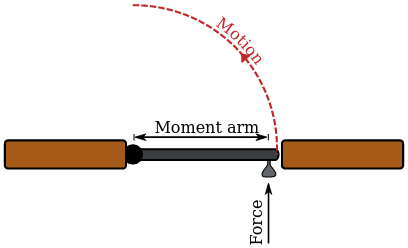
Torque
Torque, moment, moment of force, rotational force, or "turning effect" (τ) is a measure of the force that can cause an object to rotate about an axis -Newtons*meters, no joule. An object at rest remains at rest (not rotating); an object rotating, continues to rotate with constant angular velocity; unless acted on by an external torque.
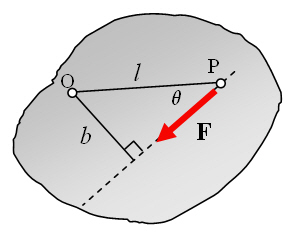
One can calculate the torque exerted by a force around an axis of rotation via
where
torque is the torque, in Newton-meters
force is the force applied, in Newtons
a lever arm is the "effective distance" from the point
of force to the axis of rotationJust as a force is what causes an object to accelerate in linear kinematics, torque is what causes an object to acquire angular acceleration.
Torque is a vector quantity. The direction of the torque vector depends on the direction of the force on the axis.
Anyone who has ever opened a door has an intuitive understanding of torque. When a person opens a door, they push on the side of the door farthest from the hinges. Pushing on the side closest to the hinges requires considerably more force. Although the work done is the same in both cases (the larger force would be applied over a smaller distance) people generally prefer to apply less force, hence the usual location of the door handle.
Rotational Equilibrium
Worked examples
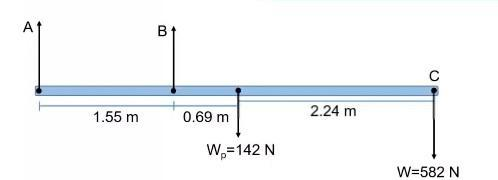
- Una clavadista de 582 N de peso esta en la punta de un trampolín uniforme de 4.48m y de 142 N. El trampolín esta sostenido por dos pedestales separados una distancia de 1.55m. Calcule la fuerza de compresión en los dos pedestales.
Planning
- We draw diagrams.
First, the effective distance is L=4.48m. Thus, La=0, La=1.55m...
Second, gravity center is L/2=2.24m by uniform springboard.
- We'll use Newton's laws:
- Solve for Fb.
3. Solve for Fa
2. Two identical uniform frictionless spheres, each of weight W. Rest at the bottom of a fixed container. The line of centers of the spheres makes an angle θ with the horizontal. What is the magnitude of the force exerted on the spheres by the container bottom? What is the magnitude of the force exerted on the spheres by one side of the container? What is the magnitude of the forces exerted on the spheres by one another?
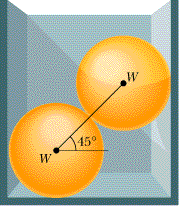
- We draw free-body diagrams.

- Modelling each shephere.
Upper sphere.
Lower shpere.
- Solve for in terms W (Spheres to bottom container).
- Solve for in terms W (Shperes to one side of the container).
- Solve for in terms W (Spheres by one another).