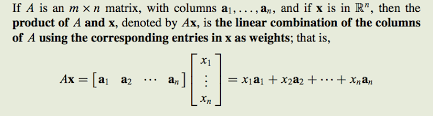Resources

Introduction

What is Linear Algebra?

Linear Algebra studies vectorial spaces and its representation as matrices. You could associate it with linear equations.

Ecosystem

Story

Related work

FAQ

Vector

A V vector is a tuple of a set of numbers in $n$-dimensional space that has $n$ components, so it lives on its vector space $\mathbb{R^n}$. The vector space consists of the set of possible vectors.

You can represent vectors geometrically, however we warning you about the limitations that you must keep in mind such as the dimensionality, magnitude, direction, relative scale, complex numbers.

https://www.desmos.com/calculator/d43yjwzrhl

You operate vectors with special sum and multiplication rules.

Let $v,w$ vectors in $\mathbb{R^n}$ the sum of vectors is defined as

https://web.ma.utexas.edu/users/ysulyma/matrix/

https://www.desmos.com/calculator/sit26yznye

Chapter 1.2.

Chapter 1.3

Chapter 2.1

Matrix

A matrix is a rectangular array (arrange a group of things in a particular way) of numbers or "entries".

The idea of Elimination

Elimination (It's a numerical method):

Ax=b ->

[(entry to eliminate*pivot) / (pivot)] - entry to eliminate ->

keep going to find all n pivots and the upper triangular U->

Ux=c -> Back substitution or breakdown

(U) Upper triangle allows back substitution.

Rules:

pivot = first nonzero.

The multiplier is l = (entry to eliminate) / (pivot) .

if pivot == 0, then you exchange. When breakdown (pivot == 0) is permanent, Ax=b has no solution or infinitely many.

Note 1:

We want to reduce, hence We subtract:

[ax -by = c] Row 1

[dx - ey = d] Row 2

Numerical Variables

c - d = (ax-by) - (dx-ey)

Note 2:

new row = Row 2 - Row 1*(entry/pivot)

= (dx-ey=d) - (ax-by=c) * (d/a)

is the same operation

Row 1 * d By d(ax-by) = dc

Row 2 * c By a(dx-ey) = ad

new row = d(ax-by) - a(dx-ey) = dc - ad

Elimination Using Matrices

Vandermonde matrix is a matrix with the terms of a geometric progression in each row.

Example: [1 1 1; 1 2 3; 1 4 9].

Rules for Matrix Operations

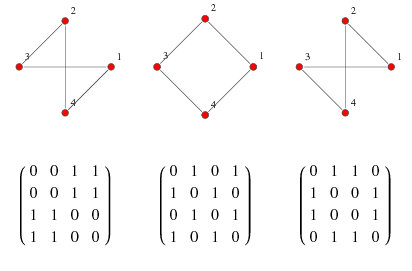
Graph or network has n nodes

Inverse matrices

Sparse matrix

In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. By contrast, if most of the elements are nonzero, then the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., m × n for an m × n matrix) is called the sparsity of the matrix (which is equal to 1 minus the density of the matrix). Using those definitions, a matrix will be sparse when its sparsity is greater than 0.5.

Hermitian, symmetric, triangular, tridiagonal, or bidiagonal

Elimination = Factorization: A=LU

L is a lower triangular product of elimination inverse and it contains the numbers $l_{ij}$. i.e. We want to factor A, not U.

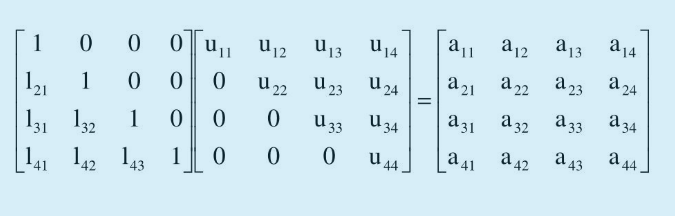
The key reason why A=LU:

$E^{-1}$ and $E$ are lower triangular. Its off-diagonal entry is $l_{ij}$ the undo the subtraction produced by $-l_{ij}$. The main diagonals contain 1's.

LDU. Lower triangular L times diagonal D times upper triangular U.

One square system.

A band matrix B has w nonzero diagonals below and above its main diagonal.

Factor: $O(n^3)$ to $O(nw^2)$. Solve: $O(n^2)$ to $O(2nw)$.

Most matrices in practice are sparce (many zero entries). In that case A=LU is much faster.

n=$10^3$. 1 second.

n=$10^4$. $10^3$ seconds.

n=$10^5$. $10^6$ seconds.

This is too expensive without a supercomputer, but that these matrices are full. Most matrices in practice are sparse (many zero entries). In that case, A=LU is much faster.

Transposes and Permutations

• Proof

  Matrix Transpose and scalar

  begingroup$ I have some problems understanding the answer in my book for this question: Let $A$ be any matrix and $k$ be a scalar. Prove that $(kA)^T=kA^T$ Books answer: "Since k is a scalar (a $1\times 1$ matrix) we have $k^T = k$ therefore $(kA)^T=A^Tk^T=A^Tk=kA^T$" Now, I understand the proof but I don't think it is valid, here are my reservations: How can you view $k$ as a scalar and a matrix at the same time?

  https://math.stackexchange.com/questions/1131826/matrix-transpose-and-scalar

  

  

• Proof

  

  If B is a vector x, such that

  $$(Ax)^T=x^TA^T$$

  $$\text{Ax combines the columns of A }$$

  $$Ax=a_1x_1+a_2x_2+...a_nx_n=b$$

  $$\text{We have }(Ax)^T=(a_1x_1+a_2x_2+...a_nx_n)^T=b^T$$

  $$(Ax)^T=(a_1x_1)^T+(a_2x_2)^T+...+(a_nx_n)^T$$

  $$(Ax)^T=a_1^Tx_1+a_2^Tx_2+...+a_n^Tx_n=[x_1 x_2 ...x_n] \begin{bmatrix} & a^T_1 &\\ & a^T_2 &\\ & . &\\ & . &\\ & . &\\ & a^T_n &\\ \end{bmatrix}$$

  $$\text{thus }(Ax)^T \text{ combines the rows of } A^T$$

  $$(Ax)^T=[x_1 x_2 ...x_n] \begin{bmatrix} & a^T_1 &\\ & a^T_2 &\\ & . &\\ & . &\\ & . &\\ & a^T_n &\\ \end{bmatrix}=x^TA^T$$

  $$\text{So }(x^TA^T) \text{ combines the rows of } A^T$$

  $$\text{In A they are columns, } A^T \text{ in they are rows.}$$

  $$([\text{column of }Ax]^T)=(\text{row of }x^TA^T)$$

  $$(Ax)^T=x^TA^T$$

  If B is $[x_1 x_2 ...]$, such that

  $$(AB)^T=\begin{bmatrix} & & \\ Ax_1 & Ax_2 & ... \\ & & \\ \end{bmatrix}^T=\begin{bmatrix} &Ax_1 & \\ & Ax_2 & \\ & . & \\&.&\\&.&\\ \end{bmatrix}=\begin{bmatrix} &x_1^TA^T & \\ & x_2^TA^T & \\ & . & \\&.&\\&.&\\ \end{bmatrix}=B^TA^T$$

• Proof

  $$I^T=I$$

  $$A^T (A^{T})^{-1}=I$$

  $$(AA^{-1})^T=I^T=I$$

  $$(A^{-1})^TA^T=I$$

  $$(A^{-1})^T=(A^T)^{-1}$$

The meaning of Inner Products

T is inside. The dot product or inner product is $x^Ty=x·y=number=<x|y>$ (1xn)(1xn)

T is outside. The rank one product or outer product is $xy^T=|x><y|=matrix$ (nx1)(1xn)

Symmetric Matrices

These are the most important matrices of all.

Permutation matrices

Definition. A permutation matrix P has the rows of the identity I in any order

Single 1 in every row and every column. There are n! permutation matrices of order n.

And $P^{-1}=P^T$

If A is invertible then a permutation P will reorder its rows for

Worked examples

1. $A^TA=0$ and $A\ne 0$ is impossible.

   $$diag(A^TA)=((col\text{ }i\text{ of }A)^T(col\text{ }i\text{ of }A))_{ii}\geq0 \\ \text{ }A^TA=0\\ diag(A^TA)=0\\ ((col\text{ }i\text{ of }A)^T(col\text{ }i\text{ of }A))_{ii}=0\\ (col\text{ }i\text{ of }A)=0\\ A=0$$

2. Find $P^3_{3x3}=I$ (but not P = I)

3. Find $P^4_{4x4}\neq I$

4. Prove that the identity matrix cannot be te product of three row exchanges (or five). It can be the product of two exchanges (or four).

We have a permutation matrix $E_p$ with only two rows distinct to $I$. It represents a row exchange.

Key properties: $E_p=(E_p)^T=(E_p)^{-1}$, $E_P^{2n}=I,E_p^{2n+1}=E_p$

Vector Spaces

This the highest level of understating about matrix calculations.

DEFINITION. The standard n-dimensional space $R^n$ consists of all column vectors $v$ with $n$ real components.

The "vectors" in S can be matrices or functions of x.

$M \text{ (2 by 2 matrices) and } F \text{ (functions) and } Z \text{ (zero vector alone) are vector spaces.}$

Properties

Max-plus vector space

An interesting “max-plus” vector space comes from the real numbers R combined with −∞. Change addition to give x + y = max(x, y) and change multiplication to
xy = usual x + y. Which y is the zero vector that gives x+0 = max(x, 0) = x for every x?

Subspace

DEFINITION. A subspace of a vector space is a set of vectors (incluiding 0) that two requirements:

If v and w are vectors in the subspace and c is any scalar, then

$v+w$ is in the subspace (additivity).

$cv$ is in the subspace. (Homogeneity of degree 1)

An operator $H$ is linear if two properties hold

$H(f_1+f_2)=H(f_1)+H(f_2)$

$H(\alpha f_1)=\alpha H (f_1)$

Worked examples

Is $max$ a linear operator?

Is the sum a linear operator?

Is the square root a linear operator?

Is the division a linear operator?

$x$

The smallest subspace

The linear span (also called the linear hull or just span) of a set S of vectors in a vector space is the smallest linear subspace that contains the set.

Column space

C(A) is a combination of r (number of pivots) columns.

Nullspace

N(A) is a combination of n-r special solutions.

Numerical Linear Algebra

Eigenvectors and eigenvalues

Eigenfunctions

Least algebras

https://textbooks.math.gatech.edu/ila/least-squares.html

Linear Regression

https://twitter.com/leonpalafox/status/1676246463389618176

Simple problems

https://www.algebra.com/algebra/homework/word/age/Really-intricate-age-word-problem.lesson

A father is 27 years older than his son ten years ago he was twice as old as his son how old is the father?

Model.

$father-27=son$

$0.5(father-10)=son-10$

So,

$father=64$

Four years ago, a mother was 4 times as old as her son. In 4 years’ time, the sum of their ages will be 56 years. Find the age of the mother when the son was born.

Model.

m-4=4(s-4)

m+4+s+4=56

The answer is m-s.

Next steps

Matrix Methods in Data Analysis, Signal Processing, and Machine Learning

References