Exam
What is parsing?
It is a compiler process that verifies if grammar can generate the string of tokens from the lexical analyzer and meanwhile it constructs a parse tree.
Describe regular language limitations and context-free grammar characteristics.
By the theory of computation results, we know that context-free grammars describe more languages than regular languages, informally we say regular languages “don’t cannot count” but CFG can instead. A prototypical language example is , where CFG handles it, but regular languages don’t.
CFG consists of a set of non-terminals, a set of terminals, a start symbol, and a set of production rules in form , where is an arbitrary string of symbols in , and is a single nonterminal.
How do we know if a grammar is ambiguous? Provide an example.
Grammar is ambiguous when it produces more than one parse tree for some string.
Example.
Let , where the rest are non-terminal symbols, the grammar production rule are
The grammar produces two distinct derivations for the string :
Therefore, it is ambiguous grammar.
Provide context-free grammar for
the language
G:
where A,S, C are nonterminals, and the rest terminal symbols.
Explanation.
The production rule produces a language with ,
The production rule produces a language where the number of is equal to .
The —start—production rule produces a language where we union the language produced by and .
the language where and that contains nested sums with different separators between them.
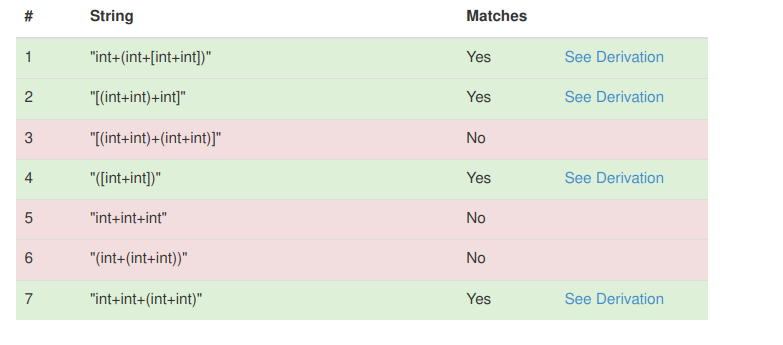
Correct cases:
[(int + int) + int]
int + [int + (int + int)]
* [( int + int ) + (int + int)] We don’t handle this, because it doesn't handle the problem definition.
Bad cases:
int + int + int
(int + (int + int))
Basis: (int+int), [int+int], int+int, int+
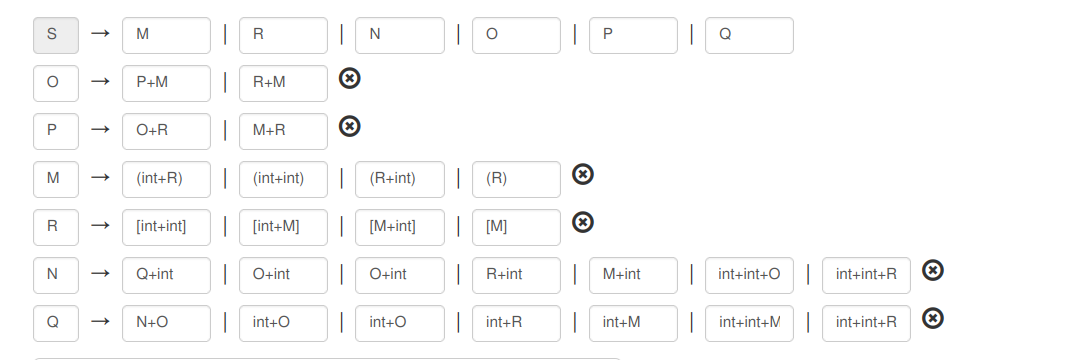
Eliminate left recursion and apply the left factoring method to the following grammar
Procedure.
We apply the left factoring method to the following grammar.
Then, we eliminate the left recursion and we got the final grammar.
Describe Top-Down and Bottom-Up parsers.
The compiler community classifies parsing strategies by how they build the parse tree.
The top-down parsers build the parse tree from the start symbol (root) to the tokens (leaves) in preorder.
The bottom-up parsers build the parse tree from the tokens (leaves) to the start symbol (root). They are more general, just as efficient, and more preferred in practice than top-down parsers.
In both cases, the parser scans the symbol stream left-to-right, one by one. Therefore, we see terminals in order of appearance.
How many parse trees are for the string “a and a or a”?
Let the following a context-free grammar
where and are non-terminals, S is the start symbol, and , , are terminals. Ignore blanks.
How many parse trees are for the string ?
The string generates 6 parse trees.
Proof.
We’re going to count how many derivations are possible from the start symbol
Here, we have two options or for each , so the string generates parse tree.
Build a LR(1) parser
Let a context free grammar with where its production rules are
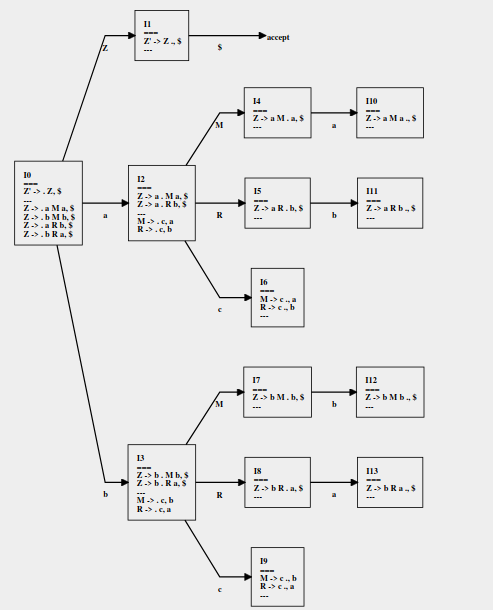
Build a DFA parsing.
State 0. ()
We begin computing the closure of {[S→.Z,$]}. We match every item with .
| Item | A | | B | | a | Comment |
| [S→.Z, $] | S | | Z | | $ | Function CLOSURE tells us to add , |
| [Z→.aMa, $] | Z | | a | Ma | $ | None of the new items has a nonterminal immediately to the right of the dot. So we have completed the state 0 or set of items 0. |
| [Z→.bMb, $] | Z | | b | Mb | $ | |
| [Z→.aRb, $] | Z | | a | Rb | $ | |
| [Z→.bRa, $] | Z | | b | Ra | $ |
Now we compute GOTO(, X) where X={Z,a,M,b,R,c} (all grammar symbols with no augmented symbol)
On X=Z go to state 1.
On X=a go to state 2.
On X=b go to state 3.
State 1. For X=Z
Since no additional closure is possible, the set of items is
It is an accepting state.
State 2. For X=a
GOTO(, X=a)=={[Z -> a.Ma, $], [Z -> a.Rb, $], [M -> .c, a], [R -> .c, b]}
On X=M go to state 4.
On X=R go to state 5.
On X=c go to state 6.
State 3. For X=b
GOTO(, X=b)={[Z→b.Mb, $], [Z→b.Ra, $], [R→.c,a], [M→.c,b]}
On X=M go to state 7.
On X=R go to state 8.
On X=c go to state 9.
The fake States. For X=M,R,c
They don’t generate new states because they were included before. We don’t mention these fake states again.
Now we are concern about new items generated by state 2 ={[Z -> a.M a, $], [Z -> a.Rb, $], [M -> .c, a], [R -> .c, b]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 4. For X=M
GOTO(, X=M)={[Z→aM.a,$]}
On X=a go to state 10.
States 5. For X=R
GOTO(, X=R)={[Z→aR.b,$]}
On X=b go to state 11.
States 6. For X=c
GOTO(, X=c)={[M -> c., a], [R -> c., b]}
It doesn’t go anywhere.
Now we are concern about new items generated by state 3 ={[Z→b.Mb, $], [Z→b.Ra, $], [R→.c,a], [M→.c,b]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 7. For X=M
GOTO(, X=M)={[Z→bM.b,$]}
On X=b go to state 12.
States 8. For X=R
GOTO(, X=R)={[Z→bR.a,$]}
On X=a go to state 13.
States 9. For X=c
GOTO(, X=c)={[R -> c., a], [M -> c., b]}
It doesn’t go anywhere.
Now we are concern about new items generated by state 4 ={[Z→aM.a,$]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 10. For X=a
GOTO(, X=a)={[Z→aMb.,$]}
It doesn’t go anywhere.
Now we are concern about new items generated by state 5 ={[Z→aR.b,$]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 11. For X=b
GOTO(, X=b)={[Z→aRb.,$] }
It doesn’t go anywhere.
Now we are concern about new items generated by state 7 ={[Z→bM.b,$]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 12. For X=b
GOTO(, X=b)={[Z→bMb.,$]}
It doesn’t go anywhere.
Now we are concern about new items generated by state 8 ={[Z→bR.a,$]}, so we call GOTO(, X) where X={Z,a,M,b,R,c}
States 13. For X=a
GOTO(, X=a)={[Z→bRa.,$]}
It doesn’t go anywhere.
Build the parsing LR(1) table.
The codes for the actions are:
- si means shift and stack state i,
- rj means reduce by the production numbered j,
- blank means error.
| STATE | ACTION | GOTO | |||||
| a | b | c | $ | M | R | Z | |
| 0 | s2 | s3 | 1 | ||||
| 1 | accept | ||||||
| 2 | s6 | 4 | 5 | ||||
| 3 | s9 | 7 | 8 | ||||
| 4 | s10 | ||||||
| 5 | s11 | ||||||
| 6 | r6 | r7 | |||||
| 7 | s12 | ||||||
| 8 | s13 | ||||||
| 9 | r7 | r6 | |||||
| 10 | r2 | ||||||
| 11 | r4 | ||||||
| 12 | r3 | ||||||
| 13 | r5 |
Show how it works with the string .
| Stack | Symbols | Input | Action |
| 0 | acb$ | shift | |
| 0 2 | a | cb$ | shift |
| 0 2 6 | ac | b$ | reduce by R→c |
| 0 2 5 | aR | b$ | shift |
| 0 2 5 11 | aRb | $ | reduce by Z→aRb |
| 0 1 | Z | $ | accept |