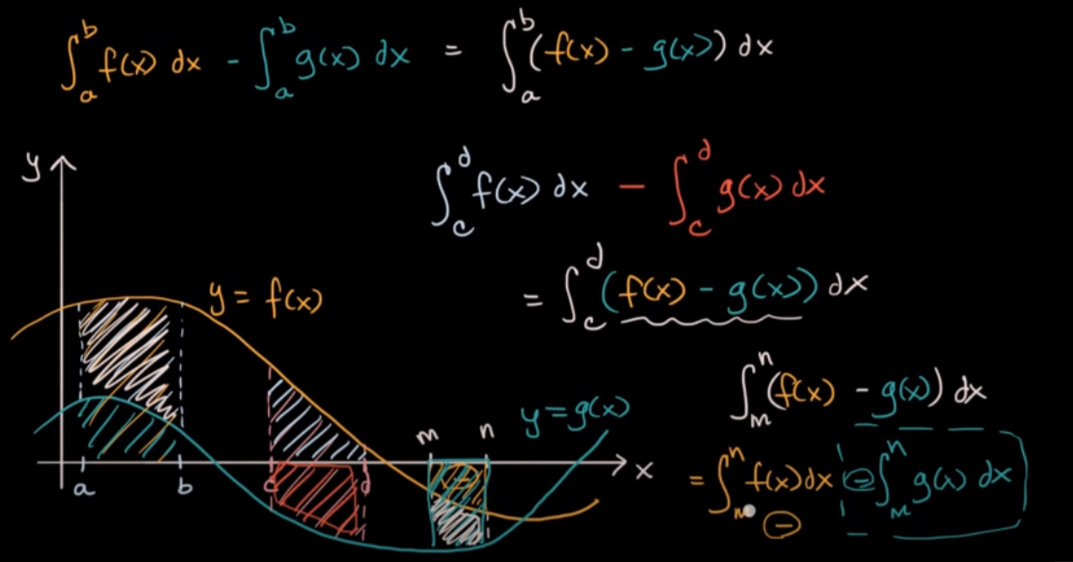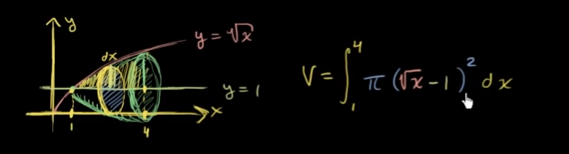➕

Calculus

Integrals

Asks
What are antiderivatives or indefinite integral?The antiderivative of a function f is differentiable F such that F'(x)=f(x). What are definite integral?Accumulation of change. What is the difference between definite integral and definite integral?


Summarize of derivatives and antiderivatives

Column 1Column 2
F(x)f(x)
|x||x|x/2
Untitled


Differential equations

Key ideasDifferencial equationsProperty
Separable differential equations: Sometimes Slope fields (graph) solving the differential equation. Exponential model:
Euler method
Untitled


Applications of integrals - Average value of a function

Applications of integrals - Numerical integration

Column 1
Key ideas
Area between curves


Limit

For any x, for any neighborhood N of f(x), there exists a neighborhood of x whose image is contained in N.

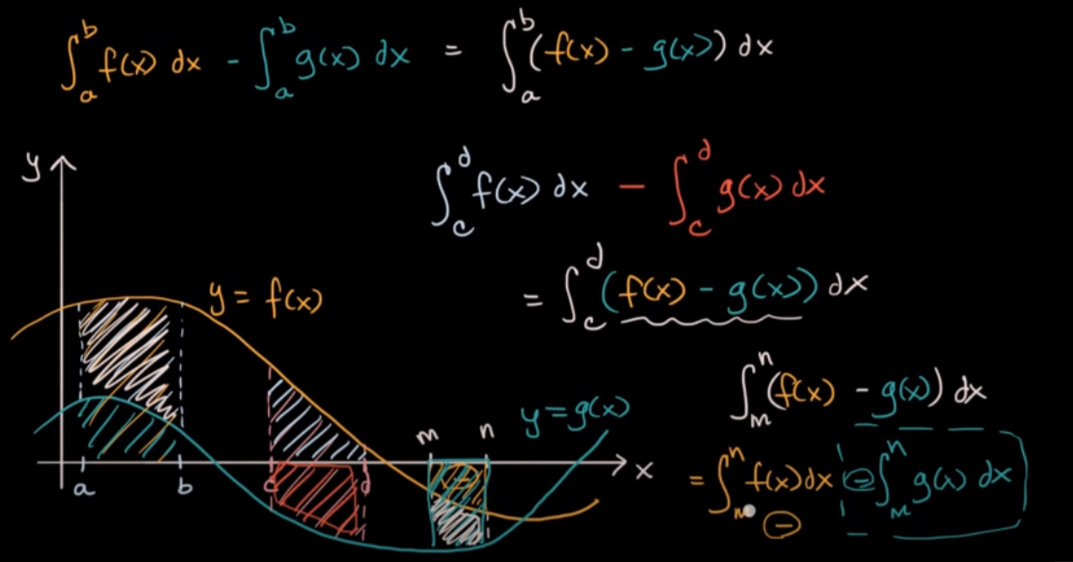
Area between curves

Theory

Planning.

∫ab∣h(x)∣dx≈b−a6[h(a)+4h(a+b2)+h(b)],where h(x)=f(x)-g(x)\int_{a}^{b} |h(x)| dx\approx \frac{b-a}{6}[h(a)+4h(\frac{a+b}{2})+h(b)] ,\text{where h(x)=f(x)-g(x)}
a,b are meetings of h, thus h(b)=0,h(a)=0a, b \text{ are meetings of h, thus } h(b)=0,h(a)=0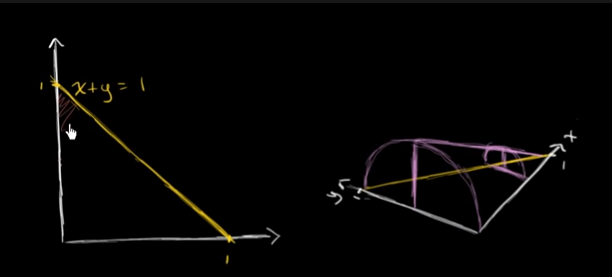
Worked example

Volume with cross-sections

∫abA(h(x))dx,A(x) from shape problem\int^b_aA(h(x))dx, A(x) \text{ from shape problem}

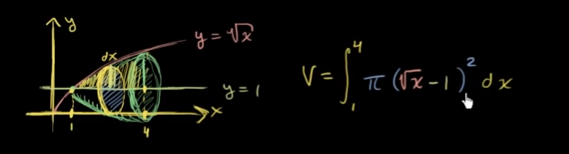
Worked examples

The volume of bodies of revolution

π∫ab∣f(x)−x′∣2dx\pi\int^b_a|f(x)-x^{'}|^2 dx
π∫ab∣f−1(x)−y′∣2dx y-axis\pi\int^b_a|f^{-1}(x)-y^{'}|^2 dx \text{ y-axis}

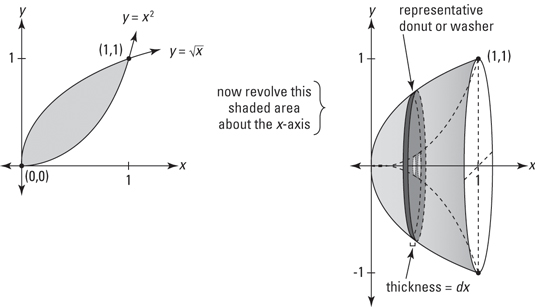
Solid of revolution between two functions

V=π∫ab∣(∣y′−f(x)∣)2−(∣y′−g(x))∣2∣dxV=\pi\int_a^b|(|y'-f(x)|)^2-(|y'-g(x))|^2|dx

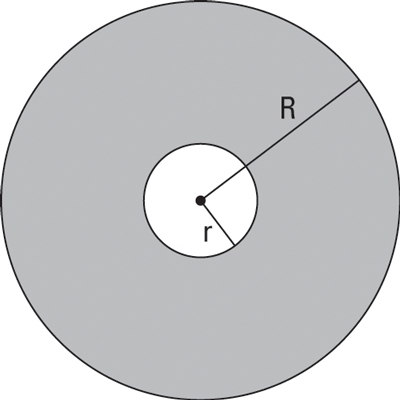
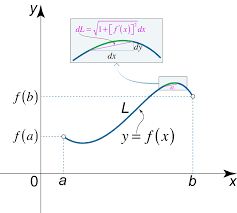
Arc length

L=∫ab1+f′(x)2L=\int_a^b\sqrt{1+f'(x)^2}

Euler Method

dydx=F′(x); F(x0)=y0\dfrac{dy}{dx}=F'(x);\text{ } F(x_0)=y_0
yyou−want=ybefore+Δystep≈ybefore+y′Δxy_{you-want}=y_{before} + \Delta y_{step}\approx y_{before}+y^{'}\Delta x

But, diferential equations are

dydx=f(x,y)∣{y,y+1,x+4+y,...}\frac{dy}{dx}=f(x,y)| \{ y, y+1,x+4+y,...\}

Thus

dydx=F′(x,y)=f(x,y); F(x0)=y0\dfrac{dy}{dx}=F'(x,y)=f(x,y);\text{ } F(x_0)=y_0
y1=F(x1)=F(x0)+F′(x0,y0)Δx=y0+f(x0,y0)Δxy_1=F(x_1)=F(x_0)+ F^{'}(x_0,y_0)\Delta x=y_0+f(x_0,y_0)\Delta x
y2(x)=y1+f(x1,y1)Δxy_2(x)=y_1+f(x_1,y_1)\Delta x
......
yn+1=yn+f(xn,yn)Δxy_{n+1}=y_n+f(x_n,y_n)\Delta x

A good approx. step is Δx=0.00001\Delta x=0.00001, meaning that we need 400,000 steps (high computational cost).

Step sizes

step sizeresult of Euler's methoderrorTitle
11638.6Untitled
0.2535.5319.07Untitled
0.145.269.34Untitled
0.0549.565.04Untitled
0.02551.982.62Untitled
0.012553.261.34Untitled


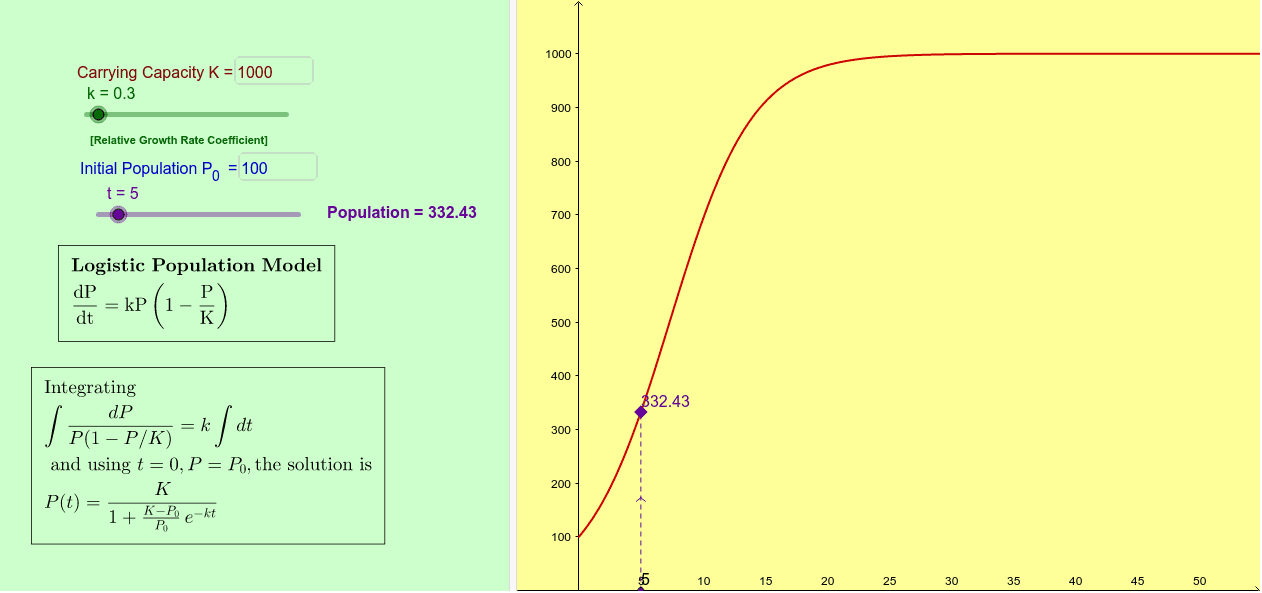
Logistic models

N(t)=N0ert,where N is the population.N(t)=N_0e^{rt}, \text{where N is the population.}
dNdt=rN(1−NK)\frac{dN}{dt}=rN(1-\frac{N}{K})

https://es.wikipedia.org/wiki/Función_logística

Partial fractions

∫P(x)Q(x)=R0ln∣q0(x)∣+...+Rnln∣qn(x)∣\int \dfrac{P(x)}{Q(x)}=R_0ln|q_0(x)|+...+R_nln|q_n(x)|
R=Q−1A−1bR=Q_{-1}A^{-1}b
Q−1=[1/q01/q1...1/qn]Q_{-1}=\begin{bmatrix} 1/q_0 & & \\ & 1/q_1 & \\ & & .&&\\ & & &.\\ & & &&.\\ & & &&&1/q_n\\ \end{bmatrix}
A=[qn...q0rn...r0]A=\begin{bmatrix} q_n & ... & q_0\\ r_n & ... & r_0 \end{bmatrix}
b=[pn...p0]b=\begin{bmatrix} p_n \\ . \\ .\\ .\\ p_0 \end{bmatrix}

Example

∫4x−11(2x−1)(x+4)dx=R0ln∣2x−1∣+R1ln∣x+4∣[124−1][R0R1]=[4−11]R=[1/21][124−1]−1[4−11]=[−13]\int \dfrac{4x-11}{(2x-1)(x+4)}dx=R_0ln|2x-1|+R_1ln|x+4|\\ \begin{bmatrix} 1 & 2 \\ 4 & -1 \end{bmatrix} \begin{bmatrix} R_0 \\ R_1 \end{bmatrix}=\begin{bmatrix} 4 \\ -11 \end{bmatrix}\\ R=\begin{bmatrix} 1/2 &\\ & 1 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 4 & -1 \end{bmatrix}^{-1}\begin{bmatrix} 4 \\ -11 \end{bmatrix}=\begin{bmatrix} -1 \\ 3 \end{bmatrix}

Summation and series

https://www.cis.rit.edu/class/simg716/series_you_should_know.pdf

https://en.wikipedia.org/wiki/List_of_mathematical_series

Definition. Given a sequence a1,a2,...,an∈Ra_1,a_2,...,a_n\in \mathbb{R},

Finite sum: ∑k=1nak=a1+a2+...+an,n≥1∑k=1nak=0,n=0\text{Finite sum: }\sum_{k=1}^{n}a_k=a_1+a_2+...+a_n,n\ge1\\ \sum_{k=1}^{n}a_k=0,n=0

But you can start with another index while exists in the sequence.

Properties

∑k=jnc=c(n−(j−1)),n≥j≥0\sum_{k=j}^nc=c(n-(j-1)),n\ge j\ge0
Linearity:∑k=1n(cak+bk)=c∑k=1nak+∑k=1nbk\text{Linearity:}\sum_{k=1}^n(ca_k+b_k)=c\sum_{k=1}^na_k+\sum_{k=1}^nb_k
Arithmetic series: ∑k=1nk=12n(n+1)\text{Arithmetic series: }\sum_{k=1}^nk=\dfrac{1}{2}n(n+1)
Sum of squares: ∑k=1nk2=n(n+1)(2n+1)6\text{Sum of squares: }\sum_{k=1}^nk^2=\dfrac{n(n+1)(2n+1)}{6}
Sum of cubes: ∑k=1nk3=n2(n+1)24\text{Sum of cubes: }\sum_{k=1}^nk^3=\dfrac{n^2(n+1)^2}{4}
Infinite sum: ∑k=1∞ak=lim⁡n→∞∑k=1nak=lim⁡n→∞f(n)\text{Infinite sum: }\sum_{k=1}^{\infty}a_k=\lim_{n\rarr \infty}\sum_{k=1}^{n}a_k=\lim_{n\rarr \infty}f(n)
Geometric series:∑k=0nxk=1+x+x2+...+xn=xn+1−1x−1,x∈R−{0}\text{Geometric series:}\sum_{k=0}^nx^k=1+x+x^2+...+x^n=\dfrac{x^{n+1}-1}{x-1},x\in\mathbb{R}-\{0\}
∑k=0∞xk=11−x,∣x∣<1\sum_{k=0}^{\infty}x^k=\dfrac{1}{1-x},|x|<1
Harmonic series: Hn=∑k=1n1k\text{Harmonic series: }H_n=\sum_{k=1}^{n}\dfrac{1}{k}
Telescoping series: ∑k=1n(ak−ak−1)=an−a0\text{Telescoping series: }\sum_{k=1}^n(a_k-a_{k-1})=a_n-a_0

Product

Definition. Given a sequence a1,a2,...,an∈Ra_1,a_2,...,a_n\in \mathbb{R},

Finite product:∏k=1nak=a1a2a3...an,n≥1,∏k=1nak=1,n=0\text{Finite product:} \prod_{k=1}^{n} a_k=a_1a_2a_3...a_n,n\ge1,\\ \prod_{k=1}^{n}a_k=1,n=0

Properties.

log2(∏k=1nak)=∑k=1nlog2(ak)log_2(\prod_{k=1}^na_k)=\sum_{k=1}^nlog_2(a_k)

Bounding summations

Worked examples

Vector calculus

↗️Vector Calculus

Differential equations

📀Differential equations

References

https://calculusmadeeasy.org/

Complex analysis